Figure 1. Statistics Budget
Last update: 10-Mar-2014 05:23 UTC
This page describes several statistics provided in the NTP specification and reference implementation and how they determine the accuracy and error measured during routine and exceptional operation. These statistics provide the following information.
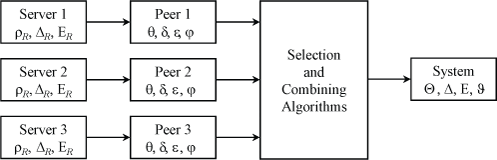
Figure 1 shows how the various measured statistics are collected and compiled to calibrate NTP performance.

Figure 1. Statistics Budget
The data represented in boxes labeled Server are contained in fields in packet received from the server. The data represented in boxes labeled Peer are computed by the on-wire protocol, as described below. The algorithms of the box labeled Selection and Combining Algorithms process the peer data to select a system peer. The System box represents summary data inherited from the system peer. These data are available to application programs and dependent downstream clients.
Each NTP synchronization source is characterized by the offset θ and delay δ samples measured by the on-wire protocol, as described on the How NTP Works page. In addition, the dispersion ε sample is initialized with the sum of the source precision ρR and the client precision ρ (not shown) as each source packet is received. The dispersion increases at a rate of 15 μs/s after that. For this purpose, the precision is equal to the latency to read the system clock. The offset, delay and dispersion are called the sample statistics.
Note. In very fast networks where the client clock frequency is not within 1 PPM or so of the the server clock frequency, the roundtrip delay may have small negative values. This is usually a temporary condition when the client is first started. When using the roundtrip delay in calculations, negative values are assumed zero.
In a window of eight (offset, delay, dispersion) samples, the algorithm described on the Clock Filter Algorithm page selects the sample with minimum delay, which generally represents the most accurate offset statistic. The selected offset sample determines the peer offset and peer delay statistics. The peer dispersion is a weighted average of the dispersion samples in the window. These quantities are recalculated as each update is received from the source. Between updates, both the sample dispersion and peer dispersion continue to grow at the same rate, 15 μs/s. Finally, the peer jitter φ is determined as the RMS differences between the offset samples in the window relative to the selected offset sample. The peer statistics are recorded by the peerstats option of the filegen command. Peer variables are displayed by the rv command of the ntpq program.
The clock filter algorithm continues to process updates in this way until the source is no longer reachable. Reachability is determined by an eight-bit shift register, which is shifted left by one bit as each poll packet is sent, with 0 replacing the vacated rightmost bit. Each time a valid update is received, the rightmost bit is set to 1. The source is considered reachable if any bit is set to 1 in the register; otherwise, it is considered unreachable. When a source becomes unreachable, a dummy sample with "infinite" dispersion is inserted in the filter window at each poll, thus displacing old samples. This causes the peer dispersion to increase eventually to infinity.
The composition of the source population and the system peer selection is redetermined as each update from each source is received. The system peer and system variables are determined as described on the Mitigation Rules and the prefer Keyword page. The system variables Θ, Δ, Ε and Φ are updated from the system peer variables of the same name and the system stratum set one greater than the system peer stratum. The system statistics are recorded by the loopstats option of the filegen command. System variables are displayed by the rv command of the ntpq program.
Although it might seem counterintuitive, a cardinal rule in the selection process is, once a sample has been selected by the clock filter algorithm, older samples are no longer selectable. This applies also to the clock select algorithm. Once the peer variables for a source have been selected, older variables of the same or other sources are no longer selectable. The reason for these rules is to limit the time delay in the clock discipline algorithm. This is necessary to preserve the optimum impulse response and thus the risetime and overshoot.
This means that not every sample can be used to update the peer variables, and up to seven samples can be ignored between selected samples. This fact has been carefully considered in the discipline algorithm design with due consideration for feedback loop delay and minimum sampling rate. In engineering terms, even if only one sample in eight survives, the resulting sample rate is twice the Nyquist rate at any time constant and poll interval.
This section discusses how an NTP client determines the system performance using a peer population including reference clocks and remote servers. This is determined for each peer from two statistics, peer jitter and root distance. Peer jitter is determined from various jitter components as described above. It represents the expected error in determining the clock offset estimate. Root distance represents the maximum error of the estimate due to all causes.
The root distance statistic is computed as one-half the root delay of the primary source of time; i.e., the reference clock, plus the root dispersion of that source. The root variables are included in the NTP packet header received from each source. At each update the root delay is recomputed as the sum of the root delay in the packet plus the peer delay, while the root dispersion is recomputed as the sum of the root dispersion in the packet plus the peer dispersion.
Note. In order to avoid timing loops, the root distance is adjusted to the maximum of the above computation and a minimum threshold. The minimum threshold defaults to 1 ms, but can be changed according to client preference using the mindist option of the tos command.
A source is considered selectable only if its root distance is less than the select threshold, by default 1.5 s, but can be changed according to client preference using the maxdist option of the tos command. When an upstream server loses all sources, its root distance apparent to dependent clients continues to increase. The clients are not aware of this condition and continue to accept synchronization as long as the root distance is less than the select threshold.
The root distance statistic is used by the select, cluster and mitigation algorithms. In this respect, it is sometimes called the synchronization distance often shortened simply to distance. The root distance is also used in the following ways.
The root distance thus functions as a metric in the selection and weighting of the various available sources. The strategy is to select the system peer as the source with the minimum root distance and thus the minimum maximum error. The reference implementation uses the Bellman-Ford algorithm described in the literature, where the goal is to minimize the root distance. The algorithm selects the system peer, from which the system root delay and system root dispersion are inherited.
The algorithms described on the Mitigation Rules and the prefer Keyword page deliver several important statistics. The system offset and system jitter are weighted averages computed by the clock combine algorithm. System offset is best interpreted as the maximum-likelihood estimate of the system clock offset, while system jitter, also called estimated error, is best interpreted as the expected error of this estimate. System delay is the root delay inherited from the system peer, while system dispersion is the root dispersion plus contributions due to jitter and the absolute value of the system offset.
The maximum system error, or system distance, is computed as one-half the system delay plus the system dispersion. In order to simplify discussion, certain minor contributions to the maximum error statistic are ignored. If the precision time kernel support is available, both the estimated error and maximum error are reported to user programs via the ntp_adjtime() kernel system call. See the Kernel Model for Precision Timekeeping page for further information.